
最近着目されつつあるPDF解析
一歩進んだ構造解析を取り入れてみませんか?
Click on the tabs below to explore these topics:
PDF解析に関する基礎知識
PDF(Pair Distribution Function)すなわち二体分布関数は、物質の結晶性に依らず原子間距離と配位数の情報を散乱パターンから引き出すことができます。
またRDF (Radial Distribution Function)として知られる動径分布関数のほうが馴染みのある人もいるかもしれませんが、基本的には縦軸の定義が違うだけで本質的には同じ解析になります。
PDF解析の解説に入る前に、下図に示す結晶質および非晶質のカーボンのX線散乱パターンを用いた測定例を見てみましょう† 。
(† 提供: 東京理科大学 駒場研究室 久保田先生 現在はNIMS 所属 詳細はこちら)
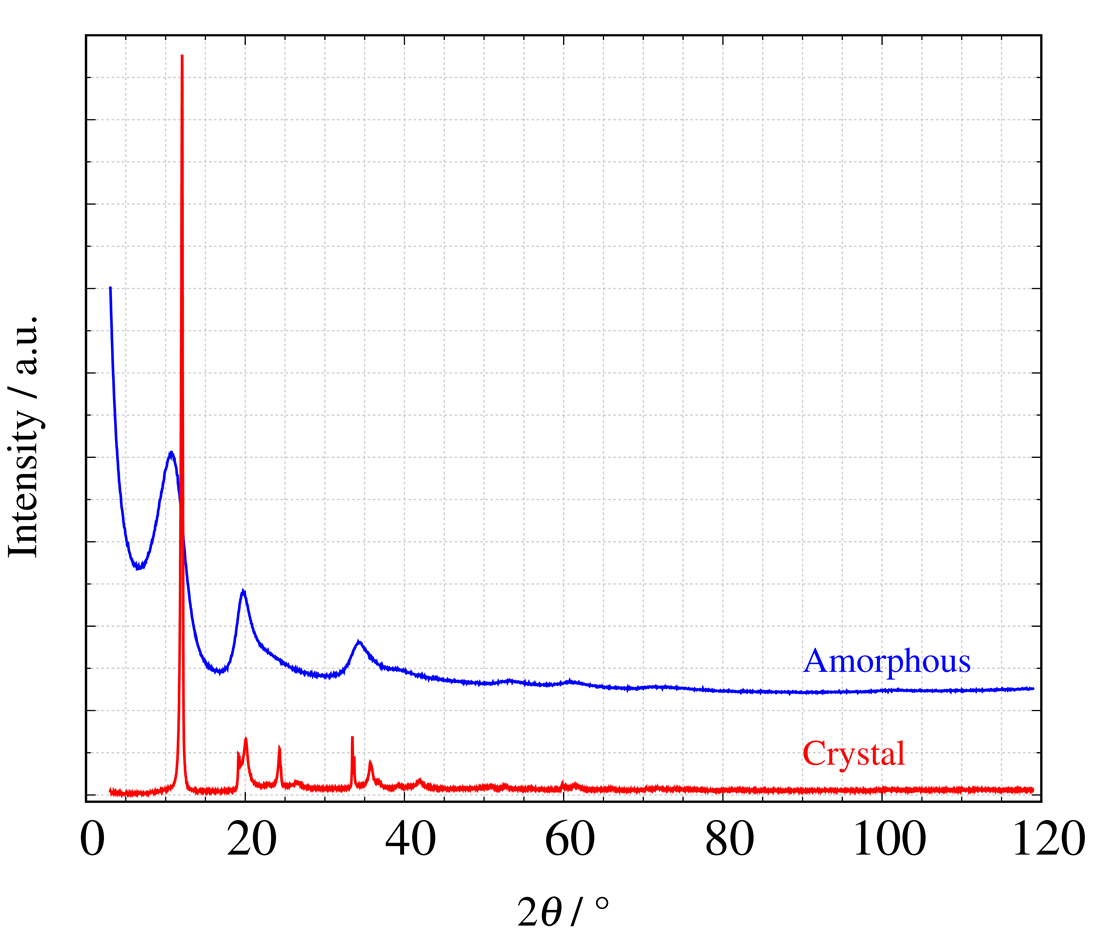
結晶質および非晶質カーボンのX線散乱プロファイル
非晶質カーボンのX線散乱パターンは、結晶質カーボンの回折パターンに比較してブロードなピークが観測されます。 このピークの正体は、試料内(原子間結合レベルのミクロな視点)に様々な距離のC-C結合が存在し、各結合距離に対応した散乱X線が互いに干渉したため観測されています。
そのため、得られた散乱パターンをフーリエ変換することで、実空間の情報を直接求めることが可能になります。 得られた実空間の情報は、縦軸は配位数や存在確率、横軸は原子間距離 r で表すことができ、実際に縦軸にRDF(配位数)、横軸に原子間距離でプロットしたプロファイルと平面として考えたカーボンの構造モデルを下図に示します。
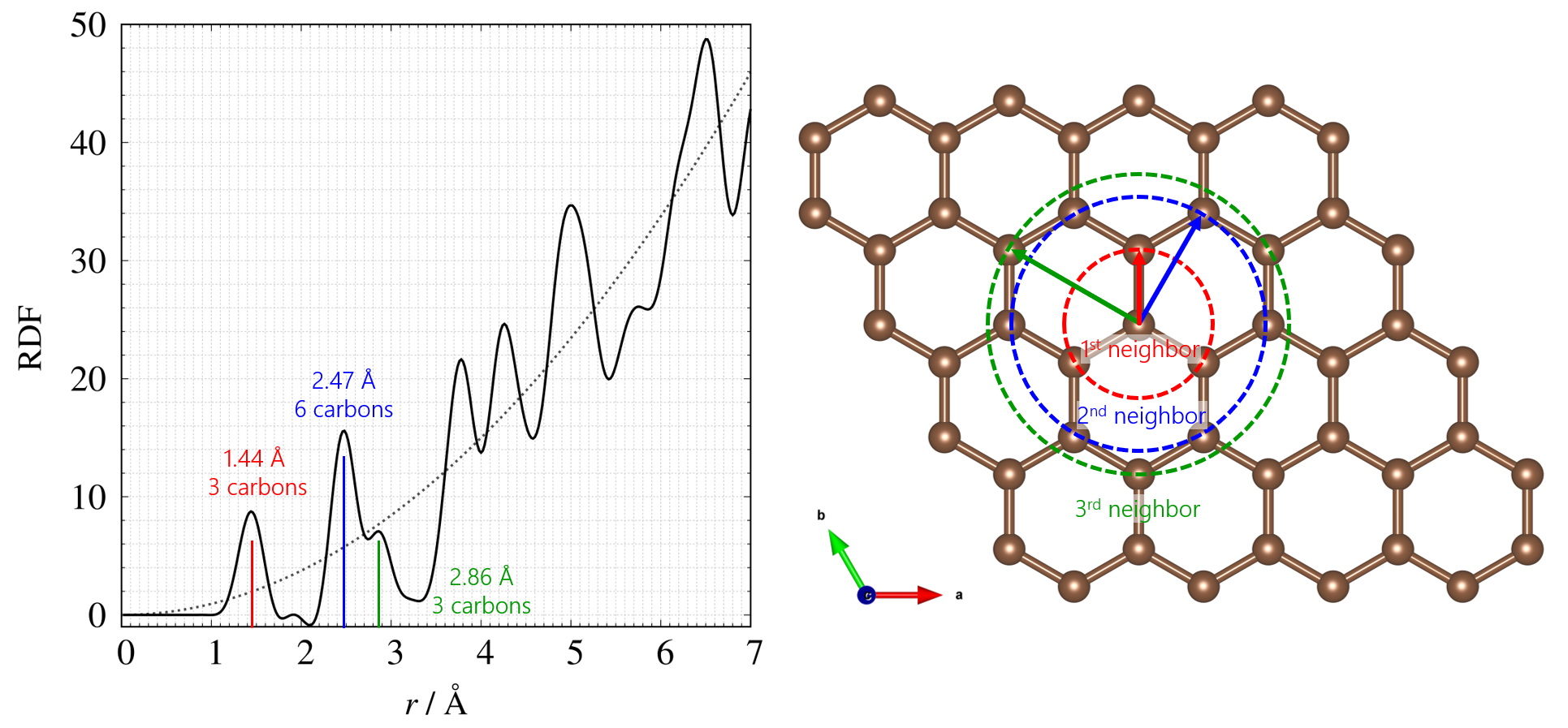
左: 非晶質カーボンのRDF、 右: 平面として考えたカーボンの構造
ピーク位置が平均原子間距離、ピーク面積が配位数に関係しています。カーボンの構造モデルを平面として考えると(実際には3次元空間の情報が導出されます)、それぞれのピーク位置から第1, 2, 3 ⋯ 隣接距離が求まります。 この性質を利用することで、非晶質系の短距離構造解析、結晶質系の局所構造の乱れ解析などに応用できるため、様々な分野での活躍が期待できる手法として期待されています。
次にもう少し具体的にPDFの算出方法を簡単に説明します。
詳しい式はリガクジャーナル1)や書籍などを参考にしてみてください。
PDFの算出方法のフローを示します。
①. プロファイル測定(全散乱測定)の実施②. 構造因子 S(Q) の算出
③. S(Q) をフーリエ変換してPDFを算出
プロファイル測定の留意点は、全散乱測定の章に纏めました。
構造因子 S(Q) は下の式から算出されます。
\begin{equation} S(Q) = \frac{I_{\mathrm{coh}} - \langle f^{2} \rangle + \langle f \rangle^{2}}{\langle f \rangle^{2}} \nonumber \end{equation} \begin{eqnarray} \langle f \rangle &= \sum_{i}^{n} c_{i}f_{i} \nonumber \\ \langle f^{2} \rangle &= \sum_{i}^{n} c_{i}f_{i}^{2} \nonumber \end{eqnarray}
ここで、ci と fi は i 番目の元素の濃度と原子散乱因子、Icoh はX線全散乱測定データから抽出した試料構造由来の干渉性散乱強度です。 干渉性散乱を抽出するために、得られたプロファイルに各種補正を行います。具体的には、バックグラウンド補正・偏光補正・吸収補正・コンプトン散乱補正を経て、原子散乱因子で規格化します。
PDF G(r) は実測した構造因子 S(Q) をフーリエ変換から得ることができます。 SiO2ガラスを例に代表的な4つの関数の定義式2)と図を示します。 各図内の破線は系内の平均密度に関連しています。
還元2体分布関数
\begin{equation} G(r) = \frac{2}{\pi} \int^{Q_{\max}}_{Q_{\min}} {Q\{S(Q)-1\}\sin Qr} \,\mathrm{d}Q\nonumber \end{equation}

2体分布関数
\begin{equation} g(r) = \frac{1}{2\pi^2\rho_{0}r} \int^{Q_{\max}}_{Q_{\min}} {Q\{S(Q)-1\}\sin Qr} \,\mathrm{d}Q + 1\nonumber \end{equation}
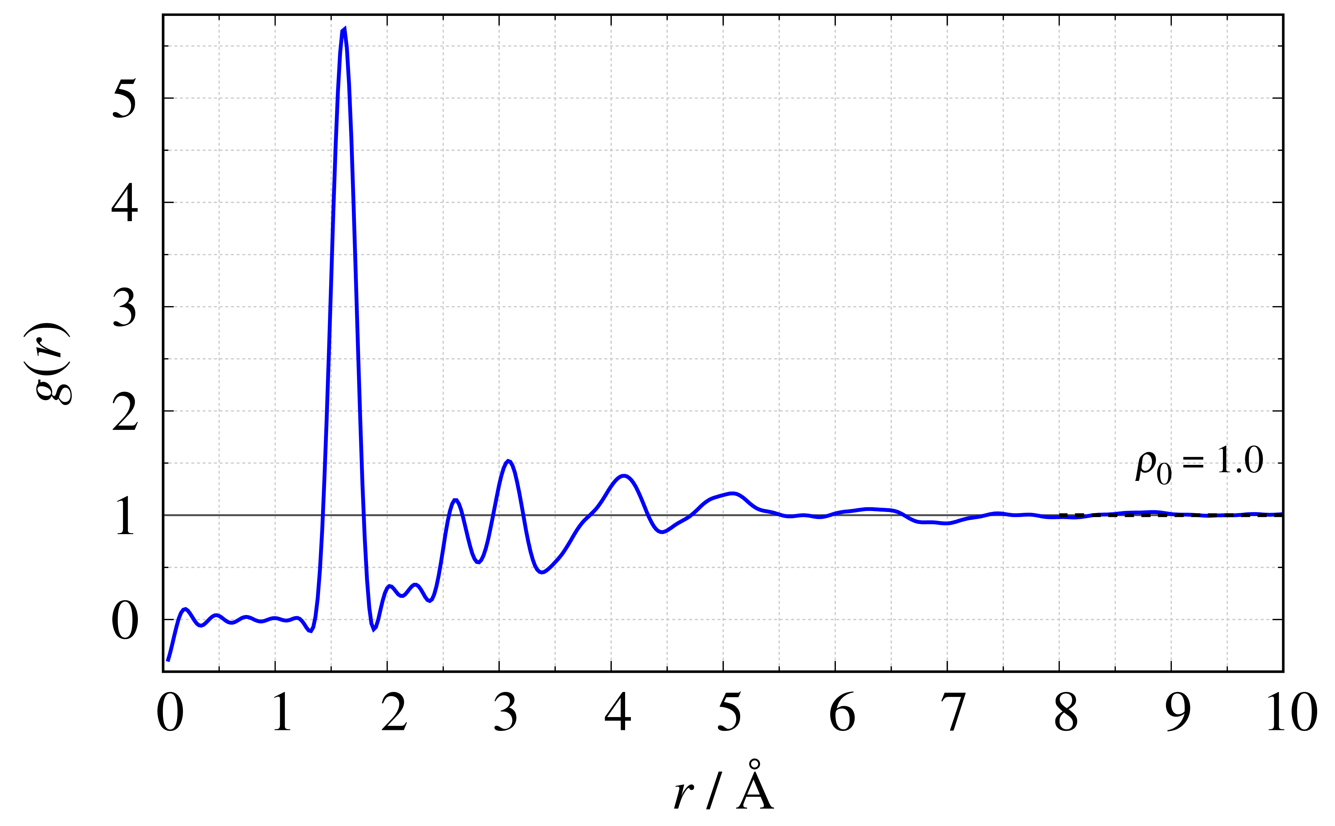
動径分布関数
\begin{equation} R(r) = \frac{2r}{\pi} \int^{Q_{\max}}_{Q_{\min}} {Q\{S(Q)-1\}\sin Qr} \,\mathrm{d}Q + 4\pi r^2\rho_{0}\nonumber \end{equation}

全相関関数
\begin{equation} T(r) = \frac{2}{\pi} \int^{Q_{\max}}_{Q_{\min}} {Q\{S(Q)-1\}\sin Qr} \,\mathrm{d}Q + 4\pi r\rho_{0}\nonumber \end{equation}
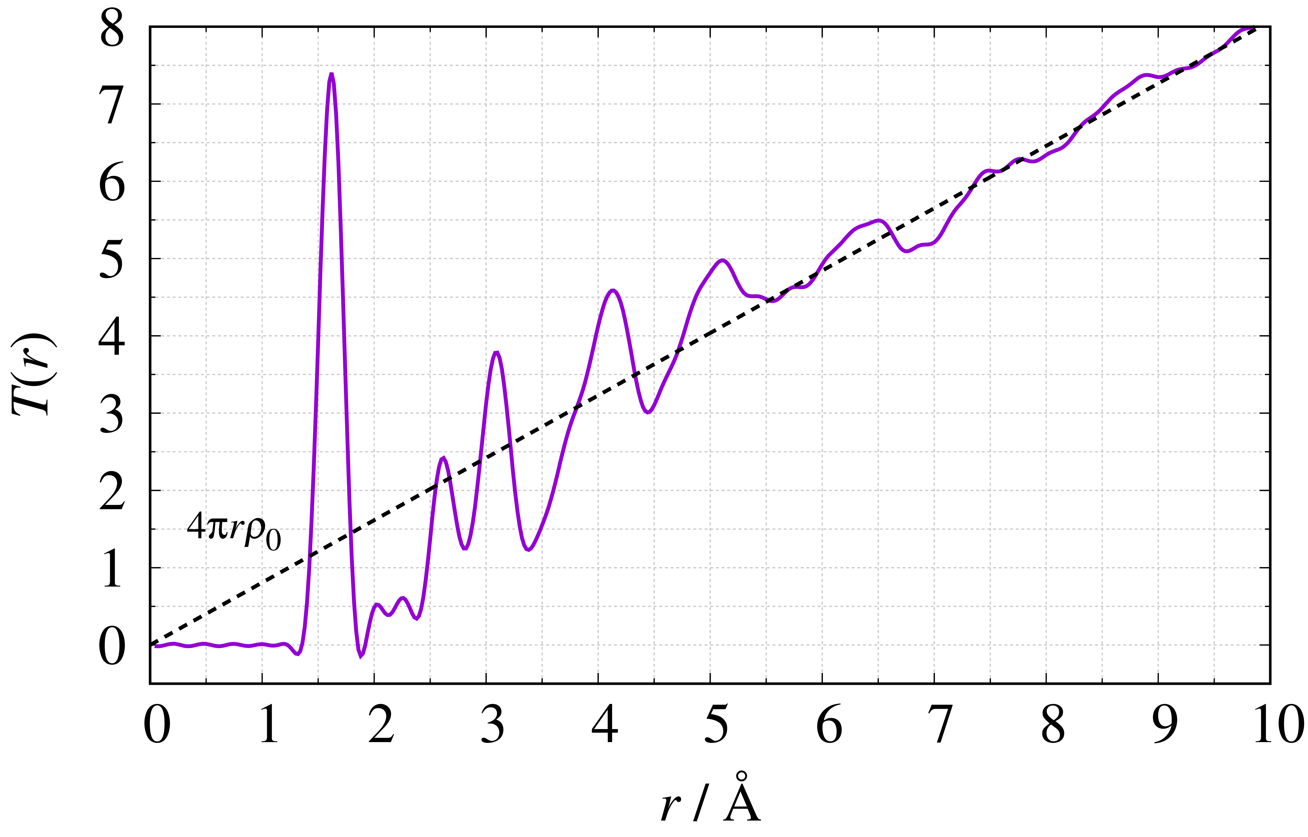
PDF解析では g(r) や G(r) を使用することが多く、非晶質は g(r) 、結晶質はG(r) を使用することが多いです。またこれらは簡単に相互変換することが出来ます。
参考文献:
[1] Y.Shiramata and M.Yoshimoto, Rigaku Journal, 50(1), (2019) 1-8.[2] D. A. Keen. J. Appl. Cryst., 34, (2001), 172. doi: 10.1107/S0021889800019993.
PDF解析用のプロファイル測定
PDF解析のための測定は、全散乱測定(Total Scattering Measurement)と呼ばれており、 その理由は、回折ピークだけではなく通常のXRD測定ではバックグランドとして取り扱われる局所構造を反映したブロードな散乱強度(散漫散乱)も解析に使用するためです。
全散乱測定のデータは、装置からの余分な散乱強度(寄生散乱)が含まれないように工夫しなければいけません。
またデータ取得のためには、3つの点に注意する必要があります。
1) X線波長
高い実空間分解能のPDFを得るためには、広い散乱ベクトル $Q$ 範囲のデータが必要です。
散乱ベクトルとは式のように定義されており、入射X線の波長が短い(高エネルギーなX線)ほど広い $Q$ 範囲のデータを測定することができます。
\begin{equation} Q = \frac{4\pi}{\lambda} \sin \theta \nonumber \end{equation}
実験室系では、$\mathrm{Mo\ K}\alpha$線や$\mathrm{Ag\ K}\alpha$線が一般的に利用されます。
$\mathrm{Cu\ K}\alpha$線, $\mathrm{Mo\ K}\alpha$線, $\mathrm{Ag\ K}\alpha$線で測定したSiO2ガラス試料を横軸 $2\theta$(左図)、横軸 $Q$ (右図)で示しました。 $\mathrm{Mo\ K}\alpha$線, $\mathrm{Ag\ K}\alpha$線では同じ$2\theta$角度でも$\mathrm{Cu\ K}\alpha$線よりも広い範囲の全散乱強度を測定できていることが分かります。
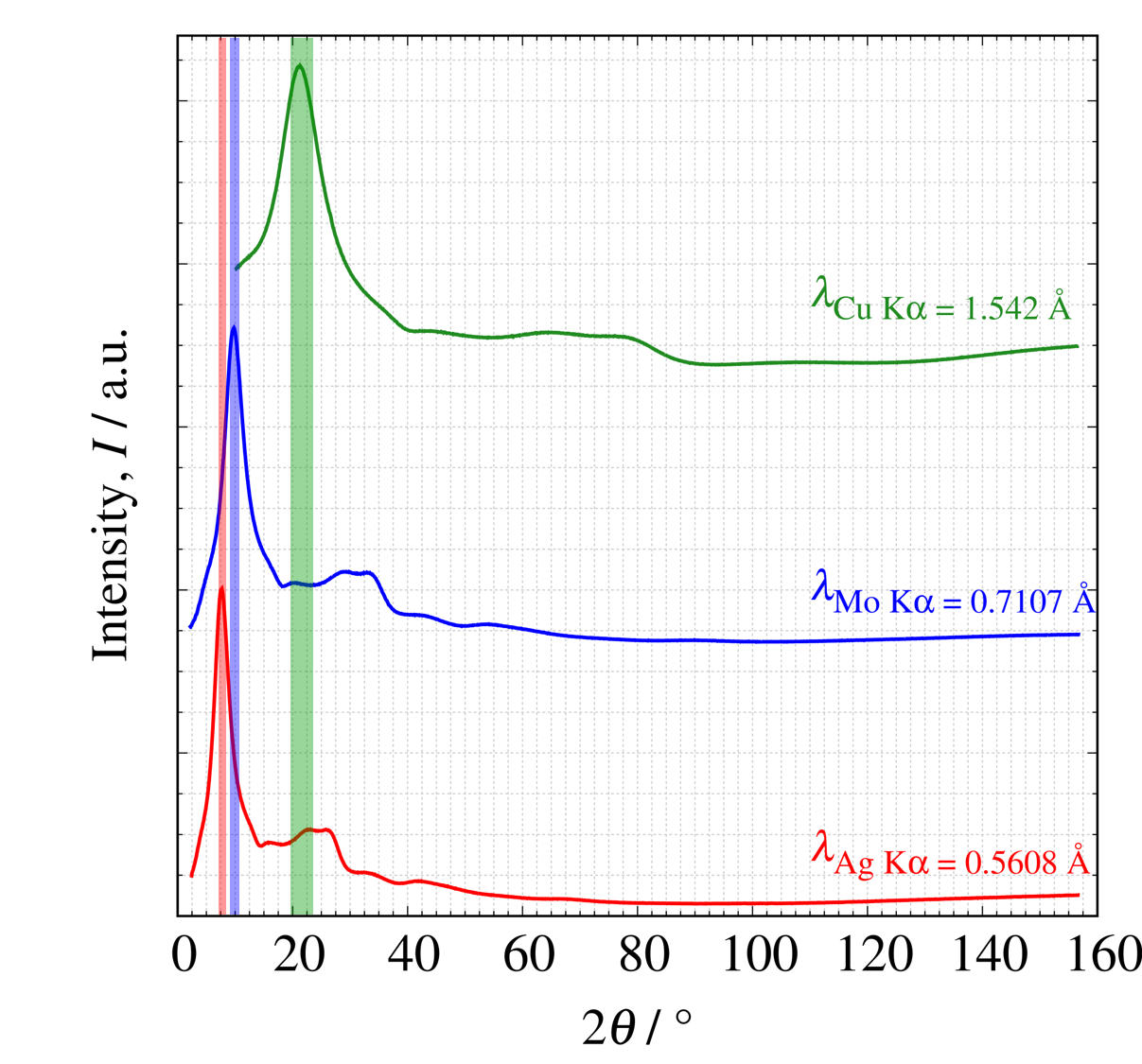

各波長で測定したSiO2ガラスのプロファイル(左: 横軸 $2\theta$、右: 横軸 $Q$ )
では、広い $Q$ 範囲の全散乱を測定するメリットとは何なのでしょうか?
それは、全散乱強度をフーリエ変換することで得られるPDF $G(r)$のピーク幅は、測定した $Q$ の最大値 $Q_{\max}$での打切り誤差が畳み込まれために広がってしまいます。
$Q_{\max}$での打切り誤差によるピーク幅の広がりは実空間分解能を知る指標として $\Delta r$ があり下の式で定義されています。
\begin{equation} \Delta r = \frac{\pi}{Q_{\max}} \nonumber \end{equation}
X線の場合、$2\theta=180^{\circ}$の条件を使うと簡便な$\Delta r$ の見積ることができ、測定に使ったX線の波長の$1/4$となります。
\begin{equation} \Delta r \approx \frac{\lambda}{4} \nonumber \end{equation}
測定に使ったX線の波長別のRDFを下図に示します。
どの波長でもSi-O相関が観測されているものの、$\mathrm {Mo\ K}\alpha$線, $\mathrm {Ag\ K}\alpha$線ではO-OおよびSi-Si相関のピークがあらわれているものの、 $\mathrm {Cu\ K}\alpha$線では実空間分解能が低くなるため(すなわち$\Delta r$ の値は大きくなる)本来2つのピークが1つのピークとして観測されています。 以上のことから、実験室系装置においては波長の短い$\mathrm {Mo\ K}\alpha$線や$\mathrm{Ag\ K}\alpha$線の使用を推奨しています。

各波長で測定した動径分布関数 $R(r)$
次に$\mathrm{Mo\ K}\alpha$線もしくは$\mathrm{Ag\ K}\alpha$線どちらの波長を選択すればよいのか考えてみたいと思います。
先に述べた通り、実空間分解能$\Delta r$ の高い$\mathrm{Ag\ K}\alpha$線のほうが全散乱測定に良いのではないか $\large{?}$ と思われるかもしれません。 しかし、測定試料によっては試料からの蛍光X線が生じ解析が困難になる場合があります。 下図には、注意するべき元素に対して相性の良い波長を示しました。

各元素に相性の良いX線の波長
下図に$\mathrm{Ag\ K}\alpha$と$\mathrm{Mo\ K}\alpha$で測定したZrO2の全散乱プロファイルを示します。 $\mathrm{Ag\ K}\alpha$で測定したデータは回折ピークによりも蛍光X線によってバックグラウンドが悪化しているのが分かります。 一方、$\mathrm {Mo\ K}\alpha$線で測定したデータでは、蛍光X線の発生が抑制され高いS/Nであることが分かります。

$\mathrm {Ag\ K}\alpha$: 青と$\mathrm{Mo\ K}\alpha$: 赤 で測定したZrO2の全散乱プロファイル
したがって、ボールミリングの材質として良く使用されるZrO2が少しでも試料に混入している可能性が高いときは、$\mathrm{Mo\ K}\alpha$ で測定したほうが良い結果が得られます。 また、検出器のディスクリミネーターを狭くして蛍光X線成分を軽減できますが、同時にコンプトン散乱成分の一部が観測されなくなってしまいPDF解析が困難なデータとなってしまいます。
測定方法(反射法もしくは透過法)および吸収補正
測定は、透過法と反射法があります。透過法が良く使用され、キャピラリー等に試料を充填して測定することが多いです。 その場合、ブランク成分として空キャピラリーのプロファイルを試料+キャピラリーのプロファイルから差し引く必要があります。 反射法の場合は、$\mathrm{Mo\ K}\alpha$線や$\mathrm{Ag\ K}\alpha$線を使用すると、試料の侵入深さが深くなり試料板からの散乱が観測されないように注意してください。 また、いずれの方法でも、試料によるX線の吸収は避けることが出来ません。 データからサンプルのみの干渉性散乱強度を正しく抽出するために正しい吸収補正を実施する必要があり、PDFプラグインでは円筒透過・平板対称透過・平板対称反射において吸収補正に対応しています(図 8)。
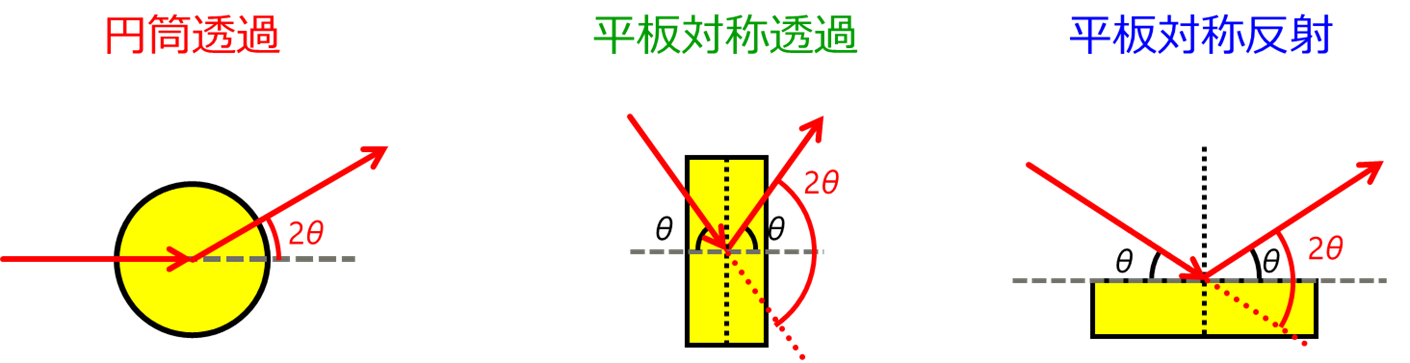
測定法の概要図
3) 測定条件(強度)
ユーザーで設定できる測定条件の中でも強度が変動するパラメーターは、走査速度やサンプリング間隔になります。 下図に走査速度を変えて強度を変化させたSiO2ガラスの$2\theta$プロファイルとPDFプロファイルを示します。 左図中にはピークトップの強度が示されており、その色に対応する右図のPDFを見てみると低強度ほどノイズが入り込んでしまっていることが分かります。 そのため、高強度を得るための工夫が必要で、例えばX線源や検出器などの装置依存のパラメーターも重要となってきます。
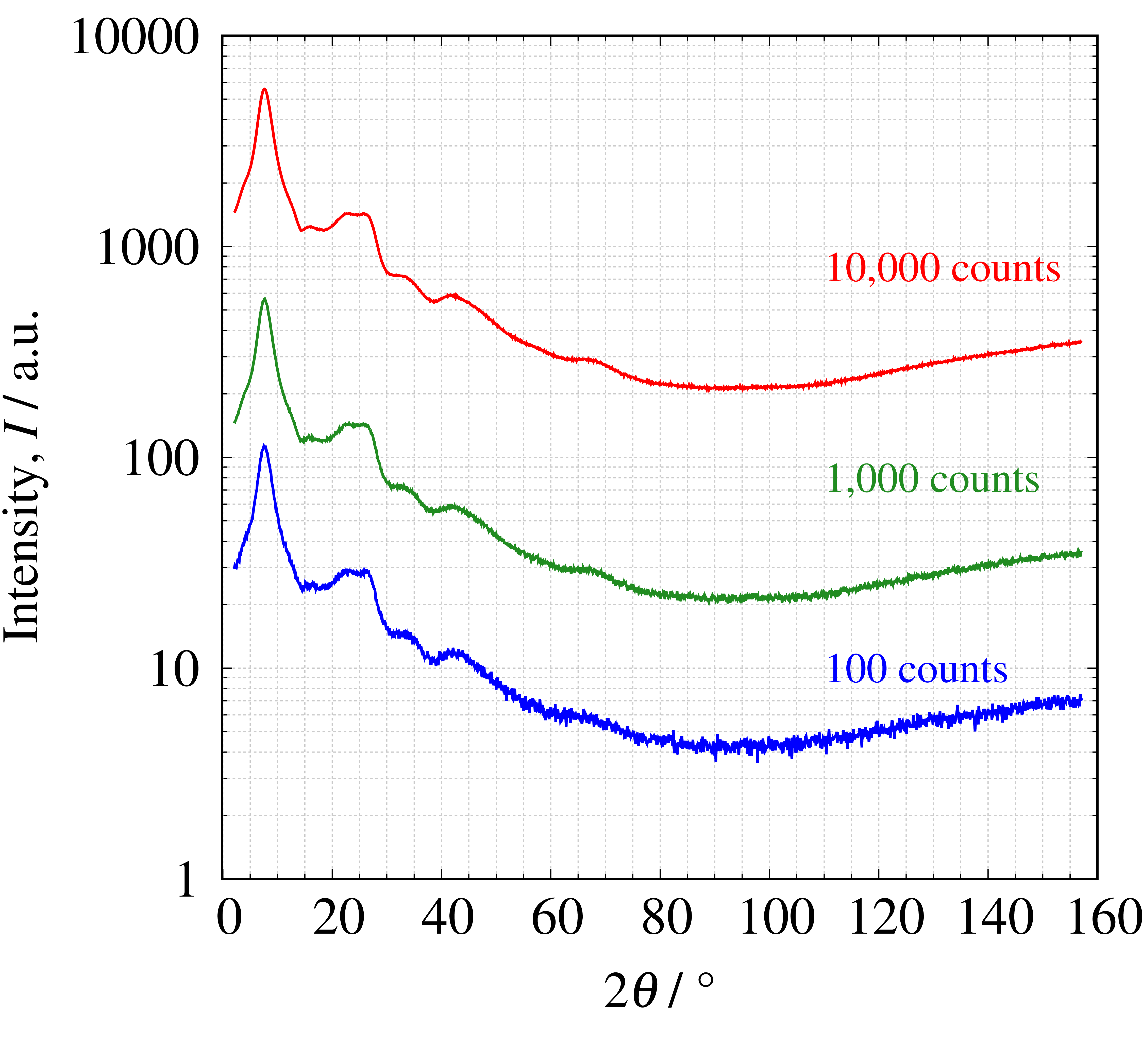

測定した$2\theta$プロファイル(左)とPDFプロファイル(右)
SmartLabの紹介
全散乱測定用の装置としての、SmartLab (ゴニオメーター) の特長を紹介したいと思います。
ゴニオメーターは、スリット類を除くとX線源、ミラー、試料部、検出器から構成されており、それらについての要素技術を説明します。
ゴニオメーター
測定角度は入射角を$0^{\circ}$に固定した状態で、$2\theta$を最大$160^{\circ}$まで動作させることが可能です (下図参照) 。またゴニオメーター半径は300 mmと長いので、角度分解能が高いです。

X線源
封入式管球・回転対陰極式管球を選択することが可能で、下の表にそれぞれの出力をまとめました。 回転対陰極式管球は実験室系装置の中でも最高出力の管球です。
表. 各ターゲットの出力一覧
| 波長 | 出力(kW) (封入管式) |
出力(kW) (回転対陰極式) |
| $\mathrm{Mo\ K}\alpha$ | 3.0 kW (60 kV-50 mA) |
9.0 kW (60 kV-150 mA) |
| $\mathrm{Ag\ K}\alpha$ | 2.16 kW (60 kV-36 mA) |
6.0 kW (60 kV-100 mA) |
多層膜ミラー
多層膜ミラーのCBO-Eを用いることで、X線ビームを検出器に集光させることが可能になります。 検出器に集光しているので、高強度・高分解能のデータを透過法で取得することが可能になります。
試料部
透過法用のキャピラリーアタッチメントを用いると、簡単に試料を取り付けることが可能です。
キャピラリーの固定方法は、図10の動画で示します。非常に簡単に設置出来ていることが分かります。
検出器
高エネルギーに対してX線検出効率の良い検出器が推奨されます。 リガクではSi素子を厚くした検出器 (D/teX Ultra250 HE, HyPix-3000 HE) を販売しています。 センサーが厚いので、高エネルギー波長に対して効率も良く、さらに${\mathrm {Cu\ K}}\alpha$などの低エネルギー波長でも検出効率を損なわず測定できます。 またPDF解析ではCdTe素子を搭載した検出器が良く宣伝されていますが、 例えば${\mathrm {Mo\ K}}\alpha$や${\mathrm {Ag\ K}}\alpha$の高エネルギー波長の吸収率は100%ではありますが、 X線の検出効率は100%でない点や、${\mathrm {Cu\ K}}\alpha$等の低エネルギー波長の検出効率は著しく低下する点に注意してください。
SmartLabと放射光施設のデータ比較
SmartLabと放射光施設(BL04B2)で測定された構造因子 $S(Q)$を図に示します。 両者は非常に良く一致していることから、SmartLabでは放射光施設と遜色ない全散乱強度を測定できることが分かります。 更にリガクではPDF解析オプションを購入された場合、SiO2ガラスの$S(Q)$を使った出荷検査しているので安心して測定・解析することが出来ます。
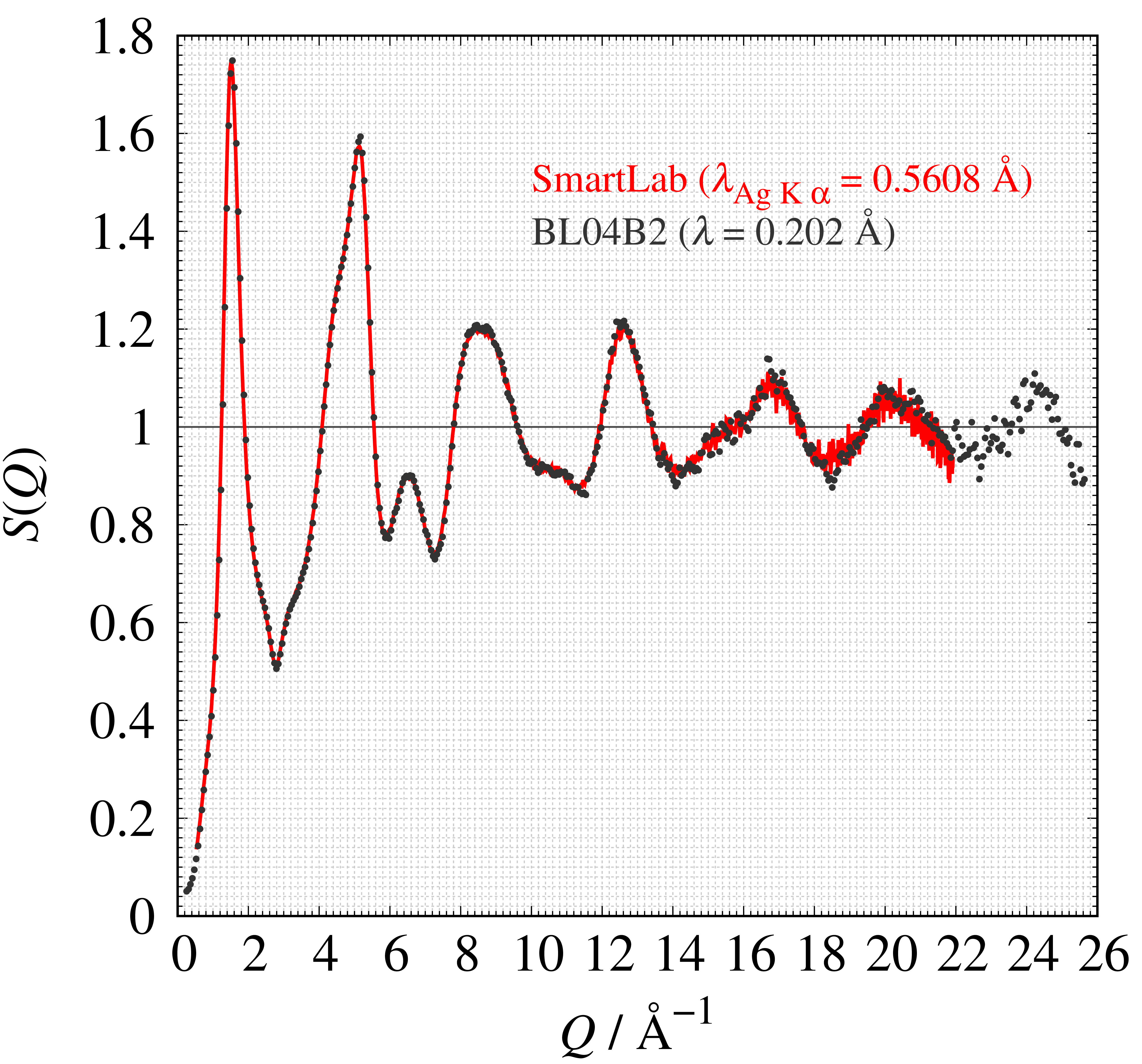
SmartLabとBL04B2 (SPring-8) で測定したSiO2ガラスの構造因子$S(Q)$の比較
SmartLab Studio $\mathrm{I\hspace{-.01em}I}$
SmartLabStudio $\mathrm{I\hspace{-.01em}I}$は測定から解析までX線分析の統合ソフトウェアです。
複数の機能の中から測定用のMeasurementプラグイン、解析用のPDFプラグインを紹介します。
Measurementプラグライン
全散乱測定においては、ミラー調整・光学系調整・キャピラリーの中心位置調整・専用の検出器エネルギーモードを備えたプロファイルの測定を実現しており、誰でも簡単に調整から測定まで実行できます。
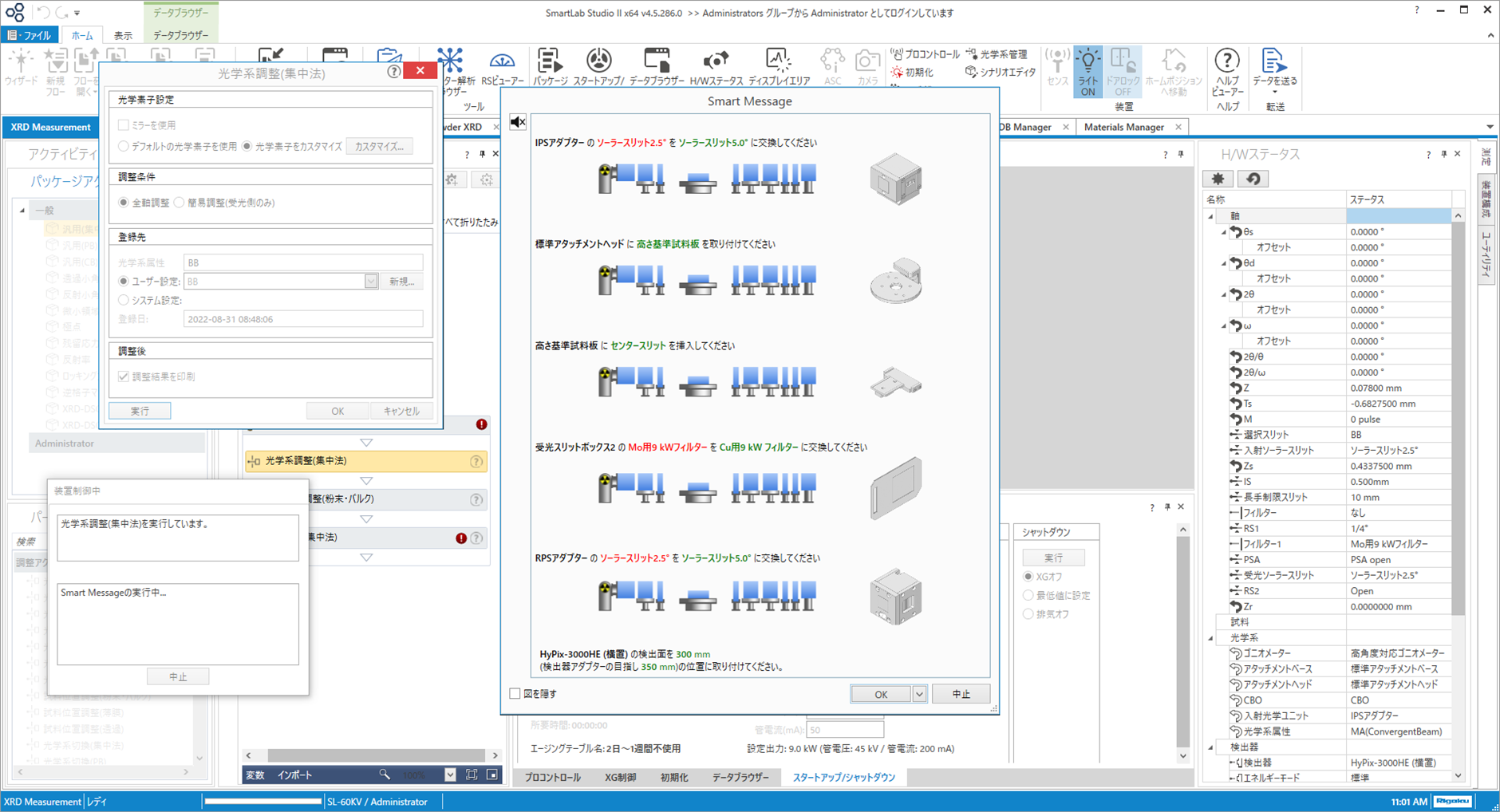
光学系調整時における素子交換の指示画面
PDFプラグイン
複雑なPDF解析の手順をフロー化し、ステップバイステップで解析を行うことが出来ます。
$S(Q)$算出、PDF算出、RMCについて紹介します。
$S(Q)$算出
$S(Q)$算出時には、コンプトン散乱成分と原子散乱成分の足し合わせた強度が表示され、試料からの干渉性散乱強度が正しく抽出できているか確認することができます。
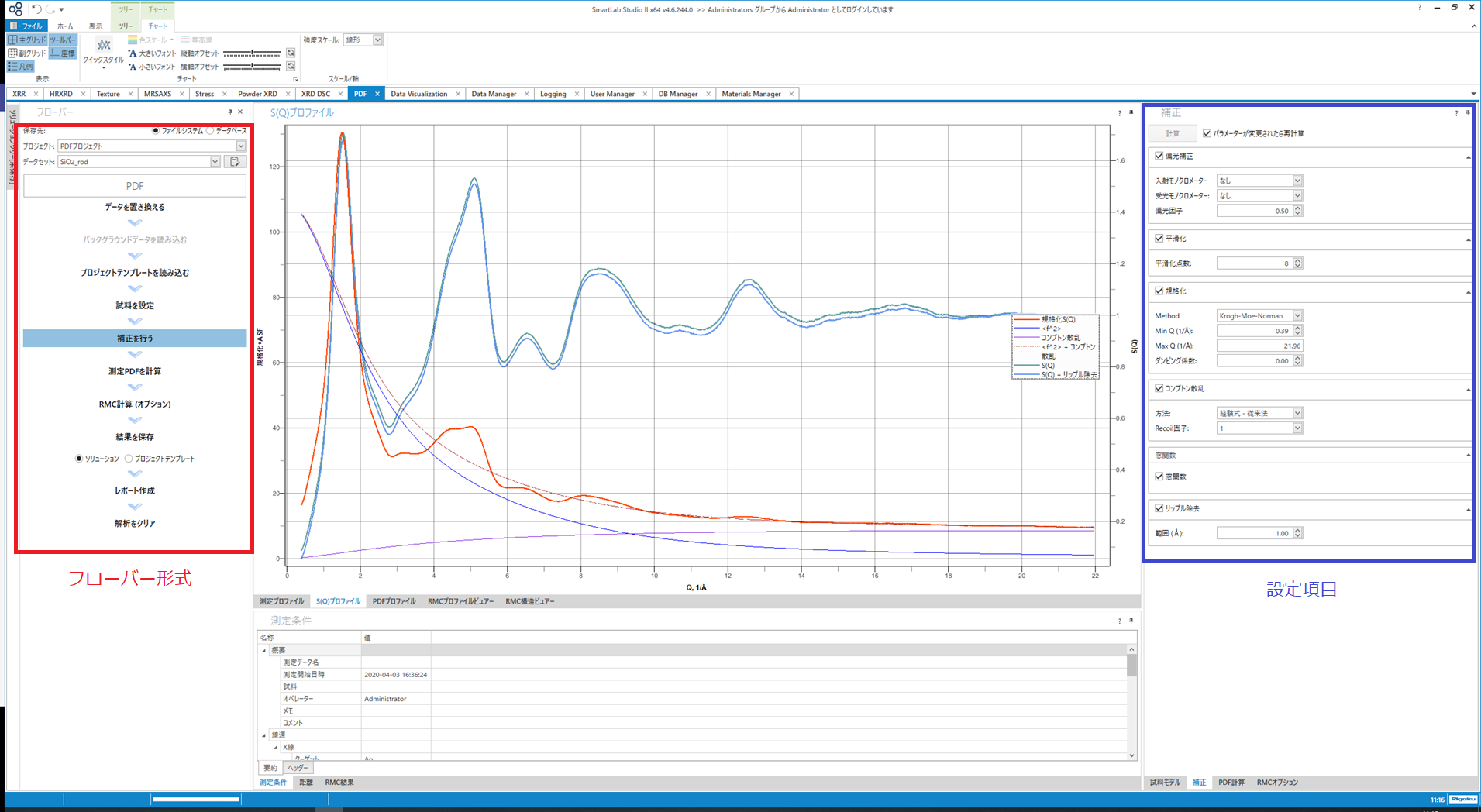
PDFプラグインの $S(Q)$算出時の画面
図 14に強度補正されたプロファイル(赤)と原子散乱因子(黒)に一致しているかどうかの例を示します。 一致していると、強度補正されたプロファイルの中心を原子散乱因子の曲線が通っており、算出されている$S(Q)$プロファイル(緑)が第2縦軸の1の周りで周期振動します(図 14左)。 しかしそれらが一致していない場合、$S(Q)$プロファイルは右肩下がりになっており、これは試料の原子数比や吸収の計算が間違っていることが推察されます(図 14右)。
PDFプラグインでは、このように解析の良し悪しを簡単に判別することもできます。 因みに図14右のような$S(Q)$の歪みを多項式近似によりベースライン補正する機能も報告されていますが、短距離側の真の情報を欠損させてしまう可能性があるので注意が必要です。
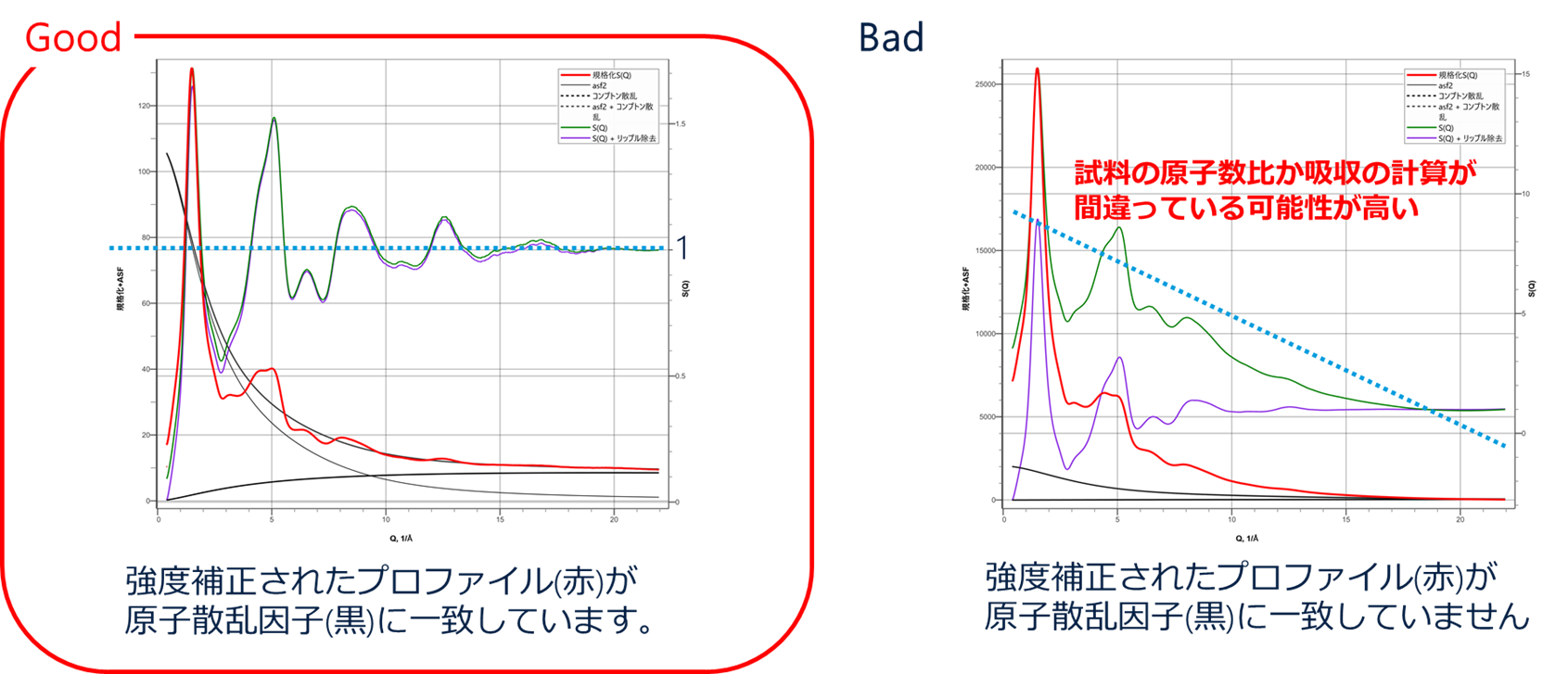
$S(Q)$算出の良し悪し 左: よい解析例、右: 悪い解析例
PDF算出
PDF算出画面を示します。結晶構造情報等があれば、自動的に結合距離を計算しプロファイルに青線で重ね書きされます。 またピーク位置もサーチされており、ピーク位置情報を簡単に知ることが出来ます。勿論、$g(r)$、$G(r)$、$R(r)$、$T(r)$の全ての関数に対応しており、相互にワンクリックで変換することが可能です。
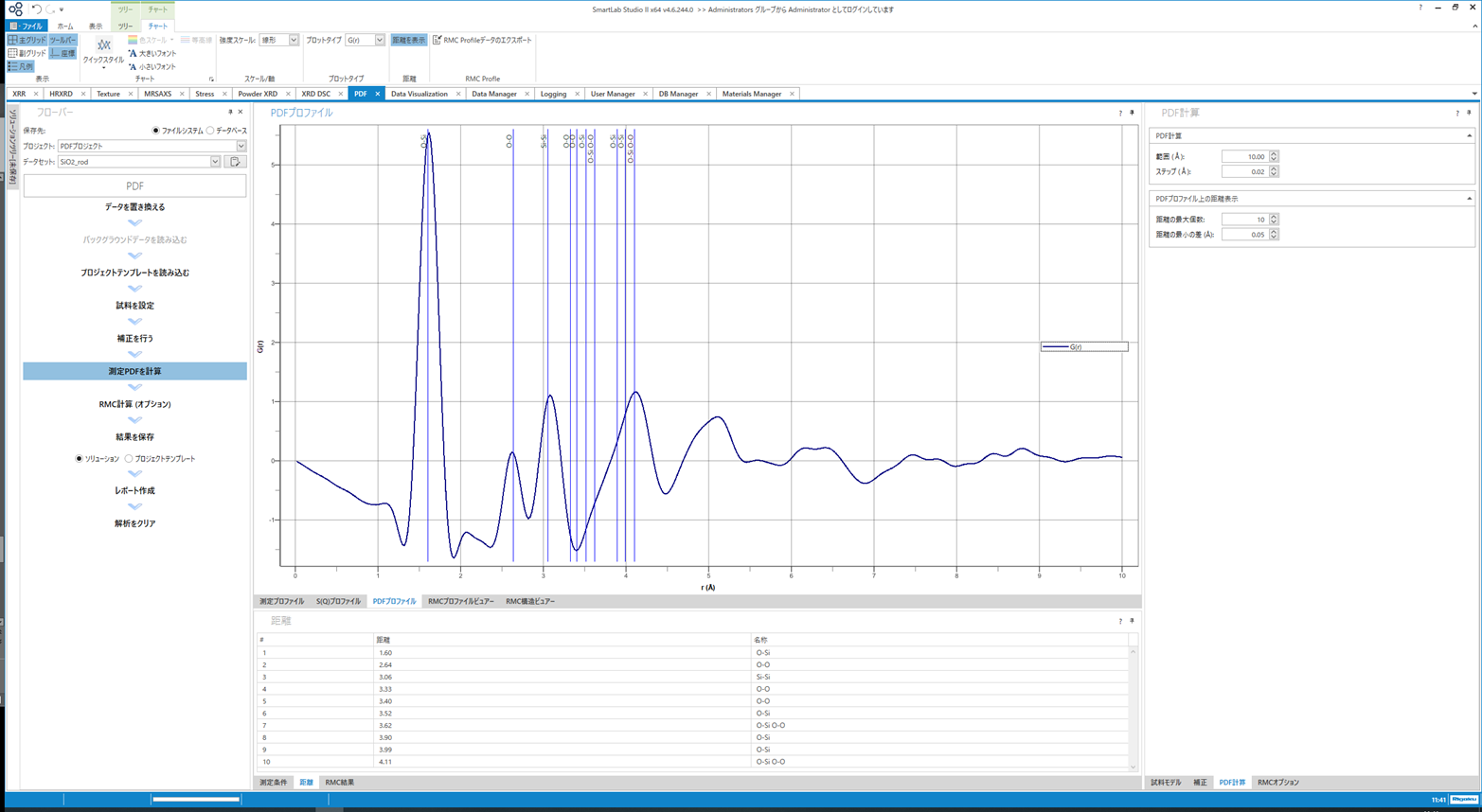
$G(r)$算出の画面
前述した多項式近似による $S(Q)$の補正とは異なり、SLS$\mathrm{I\hspace{-.01em}I}$にはリップル除去機能が搭載されています。 図にそれらの影響を $G(r)$で示します。窓関数は、フーリエ変換の打切り誤差による振動を抑制する効果があります。 リップル除去補正は、PDFプラグインの特長的な補正で設定した結合距離以下の非物理的な振動成分を $S(Q)$から除去することにより、余分な振動を$G(r)$に含めることなく算出することが出来ます。 そのことにより、$G(r)$による構造推定のフィッティング精度の向上が期待できます。
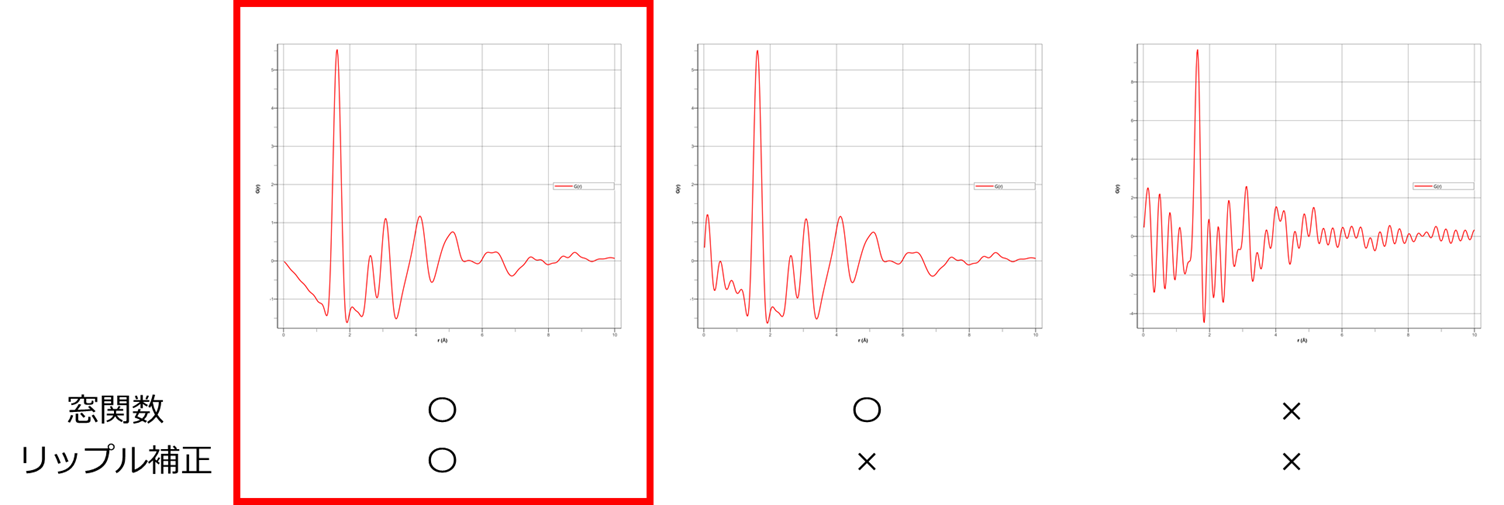
窓関数とリップル補正適用時の $G(r)$
RMC計算
RMC法のプログラムはRMCProfileが有名ですが、PDFプラグインでもRMC機能を実装しました。 現在、PDFプラグインに実装されているRMCは結晶構造中の局所構造を推定に対応しています。 従来のRMCではパラメーターの設定が難しく、RMCの使い方を習熟するには多大な時間を要していました。 しかし、PDFプラグインに実装されたRMCでは自動的にパラメーターを設定する為、必要最低限のパラメーターの入力だけでRMCを実行することができます。
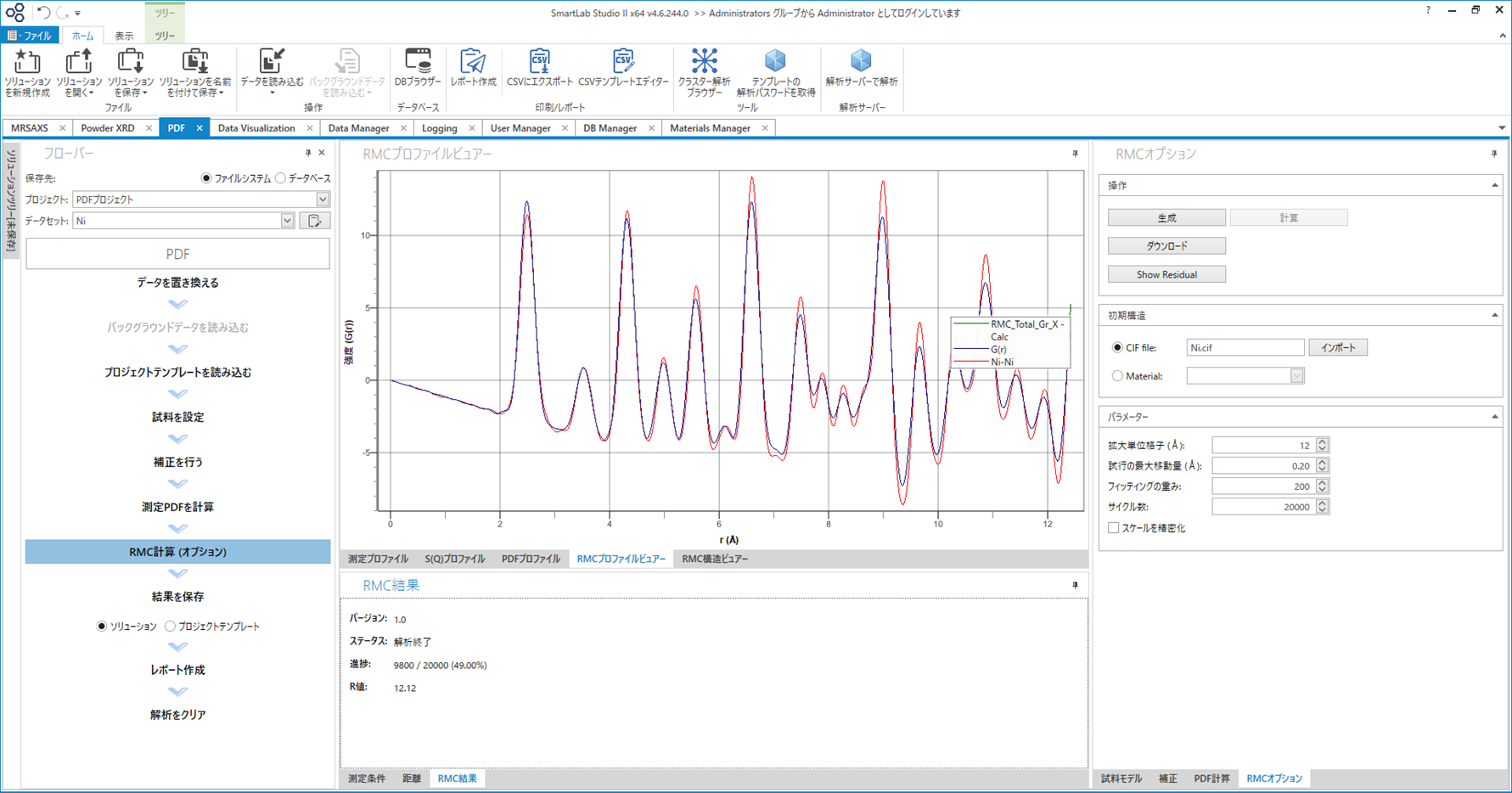
RMC実行中の画面
サンプルの密度推定
以前から第1ピーク未満 (短距離)の$G(r)$の傾きはサンプルの真密度に関連することが知られていましたが、第1ピークよりも短距離側では、$S(Q)$に含まれるにモジュレーションによるリップルが観測されるため傾きからでは精確な密度を算出することができませんでした。 そこで、$S(Q)$に含まれるモジュレーションを補正し、$G(r)$のリップルを抑制することによってサンプルの密度を求めることができるようになりました。
SiO₂ガラスの密度を全散乱データから推定した例を紹介します。図に示すのは、密度推定過程における推定密度 ρ0 と推定密度との一致度 R の変化です。 繰り返し補正することにより推定密度が一定値に近づき残差は次第に小さくなっていることが分かります。 最終的に得られた密度の値は ρ₀=0.06311 atoms⋅Å⁻³ となり,報告されているSiO₂ガラスの密度 1, 2) (ρbulk=0.06613 atoms⋅Å⁻³) と比較すると5 %未満で一致しました。
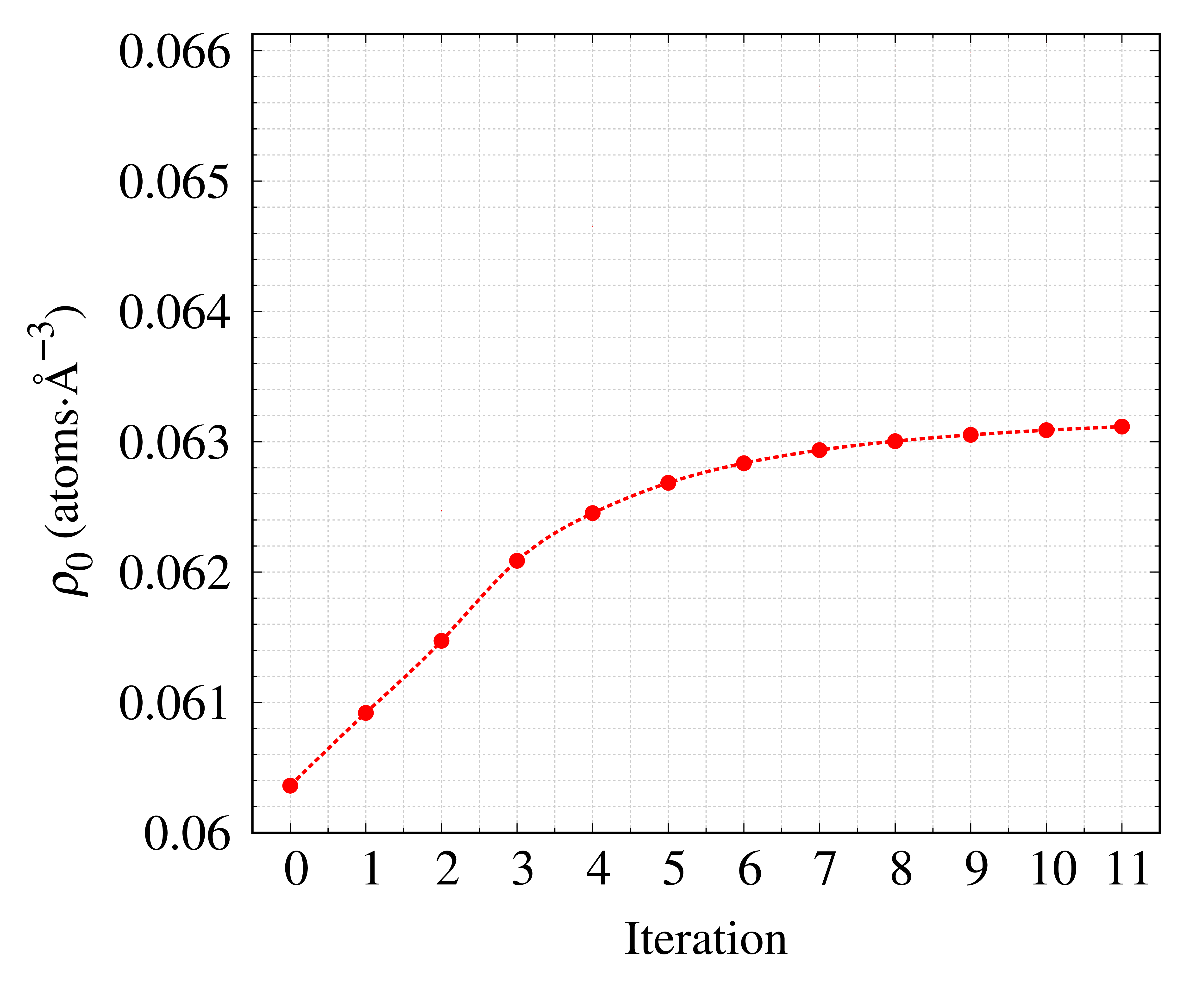

SiO2ガラスの密度推定時のイテレーション変化
次にNiの全散乱データから密度を推定したところρ₀=0.09148 atoms⋅Å⁻³ となりました。この値は格子定数から求めた密度 ρbulk=0.09132 atoms⋅Å⁻³ と非常によく一致しています。 下の図に示したのは、補正前後でのS(Q) とG(r) の比較図です。補正前後で S(Q) と G(r) は大きく変化していないことが分かります。

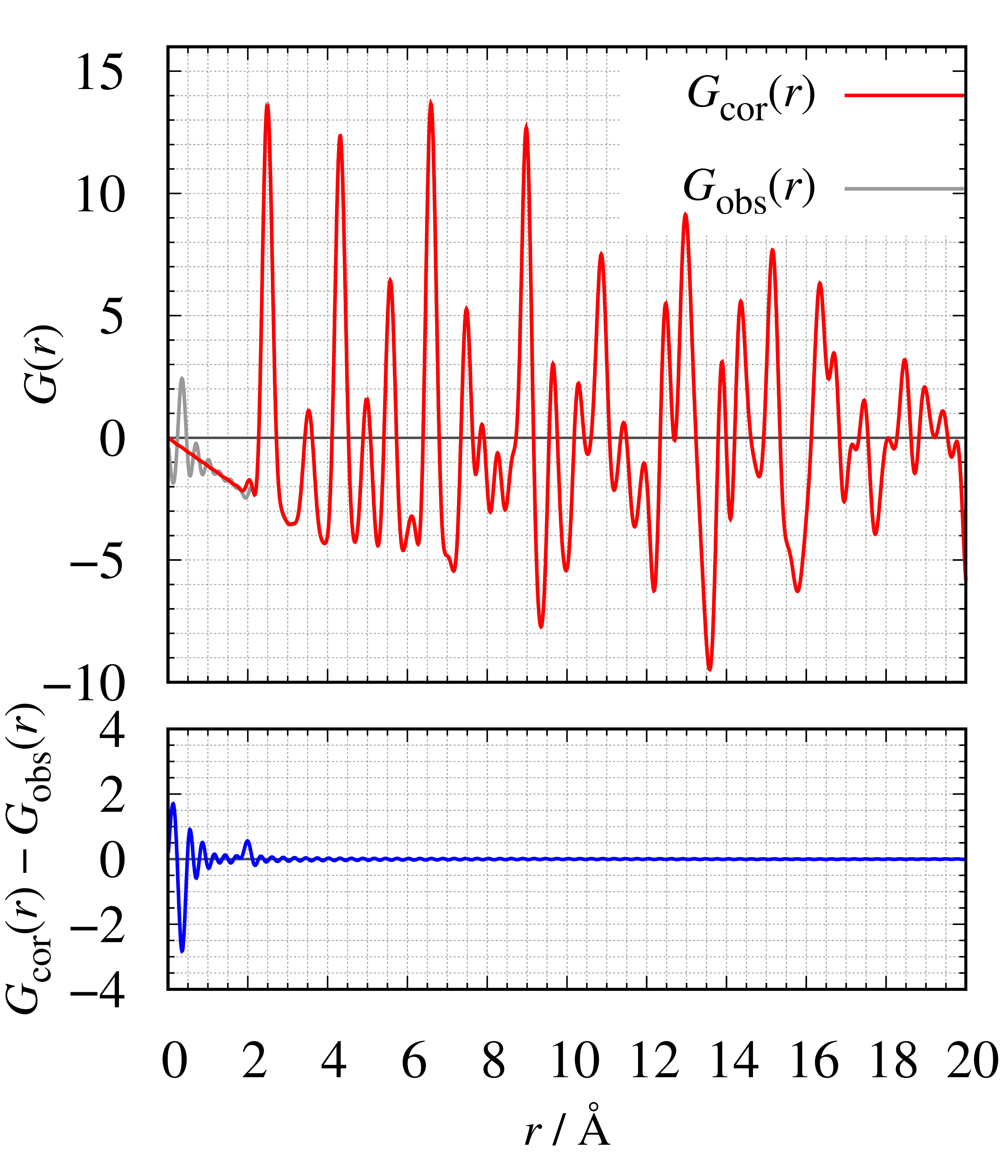
補正前後の$S(Q)(左)$と$G(r)$(右)の比較図
全散乱データによる密度推定法を用いることで、従来の密度計測法では測定困難なサンプル(禁水性のサンプルや構造中に細孔が存在する多孔質性のサンプルなど)の密度を計測することができるようになりました。
詳細な解説や解析例は文献を参考してください。
参考文献:
[1] M. Yoshimoto, K. Omote, J. Phys. Soc. Jpn. 91 (2022) 104602 (7pp). doi: 10.7566/JPSJ.91.104602[2] M.Yoshimoto, Rigaku Journal 53 (2022) 27-36.
RMC法を使った$\mathrm{LiMn_{2}O_{4}}$の局所構造解析
正極材としてよく知られているスピネル型のマンガン酸リチウム ($\mathrm{LiMn_{2}O_{4}}$ LMO)は、室温付近で構造相転移することが知られています 1, 2)。 高温相のLMO(下図 左)は、立方晶(cubic)の構造であり構造内は単一の$\mathrm{MnO_{6}}$八面体であることが知られています。 一方、低温相のLMO(下図 右)は、cubic型が$3a \times 3a \times 1a$で拡張された直方晶(Orthorhombic)で、$\mathrm{MnO_{6}}$八面体は5種類(各サイトで異なる構造)であることが知られています。 このようにユニークな特徴を持つLMOの局所構造をRMC法により解析した例を紹介します。


高温相と低温相のLMOの構造モデル図
下図に示すのは、LMOの実測値と計算値の構造因子 $S(Q)$の比較です。また、下側のプロットは実測値と計算値の残差を示しています。
RMC法を使って推定したLMOの構造モデルは実測値を良く再現していることが分かります。
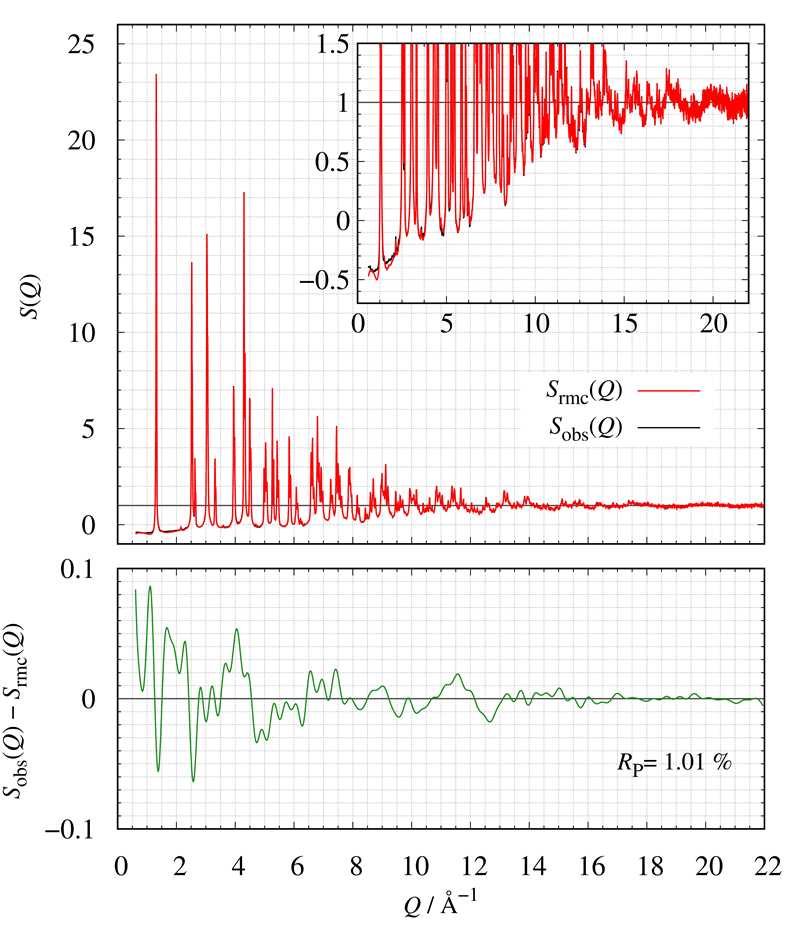
LMOの実測した$S(Q)$と計算した$S(Q)$の比較
詳細なMnの特徴量を計算するために、LMOの構造中のMn原子の価数をBVS法により算出したところ (使用したBVSパラメーター: $r_0 = 1.753 Å$,$R=0.37 Å$)、 ほとんどのMnは3価 $(58.98 \%)$ と4価$(34.96 \%)$ に分類され、残りは2価 $(5.95 \%)$ と5価 $(0.097 \%)$ に分類されました。
2価と5価の割合は低いため、これ以降の解析では取り扱いません。下図に3価と4価のO-Mn-Oの角度ヒストグラムを示します。
3価の角度ヒストグラム(青実線)は、$\theta=90^{\circ}$付近に分布が2つありますが、4価の角度ヒストグラム(赤実線)では、$\theta=90^{\circ}$付近の分布は1つになっていることが分かります。
3価と4価の角度ヒストグラムの違いは、Jahn-Teller 効果によって引き起こされていると予測されます。本解析の詳細な説明は参考文献3, 4を参照してください。

価数別のO-(Mn)-Oの角度ヒストグラム
このように、RMC法を使うことで粉末構造解析ではできなかった詳細な局所構造の解析が実施できるようになりました。
参考文献:
[1] J. Rodríguez-Carvajal, G. Rousse, C. Masquelier, M. Hervieu, Phys. Rev. Lett. 81 (1998) 4660-4663. doi: 10.1103/PhysRevLett.81.4660[2] G. Rousse, C. Masquelier, J. Rodríguez-Carvajal, E. Elkaim, J.-P. Lauriat, J.L. Martínez, Chem. Mater. 11 (1999) 3629-3635. doi: 10.1021/cm9910963
[3] M. Yoshimoto, K. Omote, Appl. Phys. Express 16 (2023) 015005 (4pp). doi: 10.35848/1882-0786/acb2b0
[4] M.Yoshimoto, Rigaku Journal, 53 (2022) 27-36.
Li3PS4の結晶化過程の局所構造変化の解析
硫化物系固体電解質であるLi3PS4は複数の相を取りガラス相、γ相、β相とα相が知られています。3つの結晶相の特徴を図に示します。
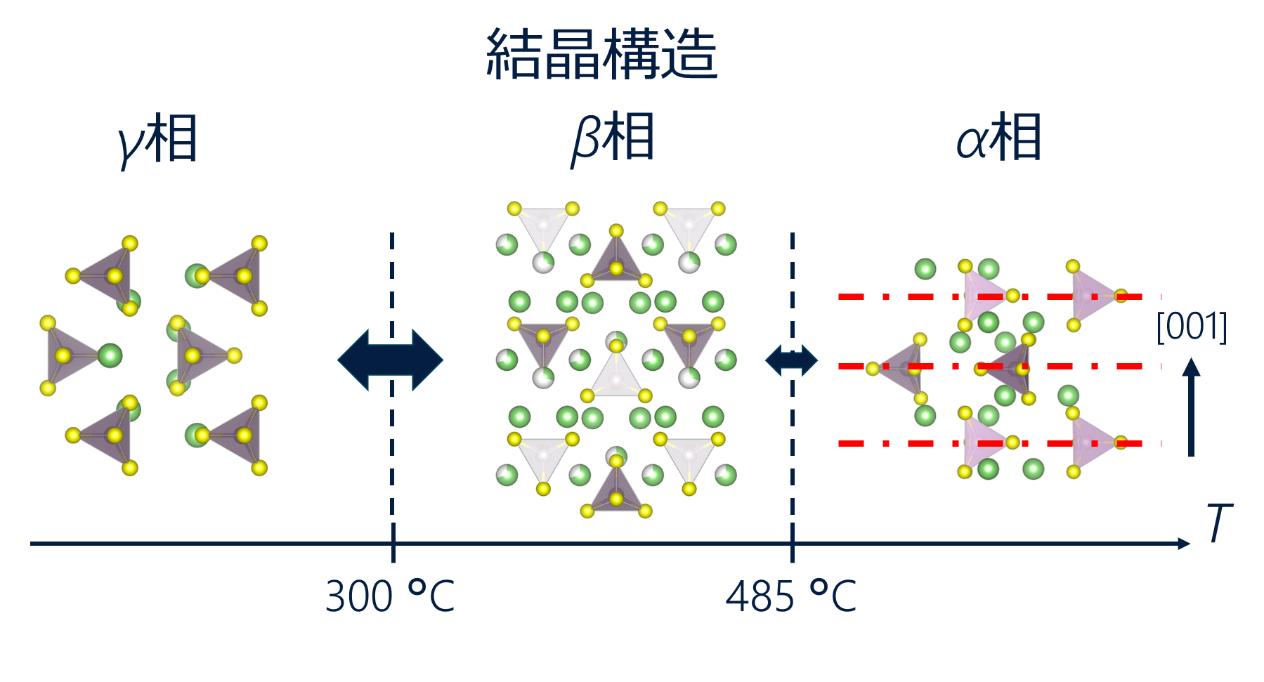
各相の結晶構造の違いと相転移温度1)
このアプリケーションでは、室温から250℃の昇温過程で全散乱測定を実施しRMC法を使って結晶化過程の局所構造の変化を可視化しました。
下図は、実測のG(r)と結晶状態(T = 250 °C,t = 75.5 h)の部分相関を比較したものです。r≥4.5 Åに現れるショルダーとピークはそれぞれP-S相関とS-S相関であることが分かります。結晶化に伴う実測のG(r)の違いがどの部分相関の影響なのかを調べることができます。
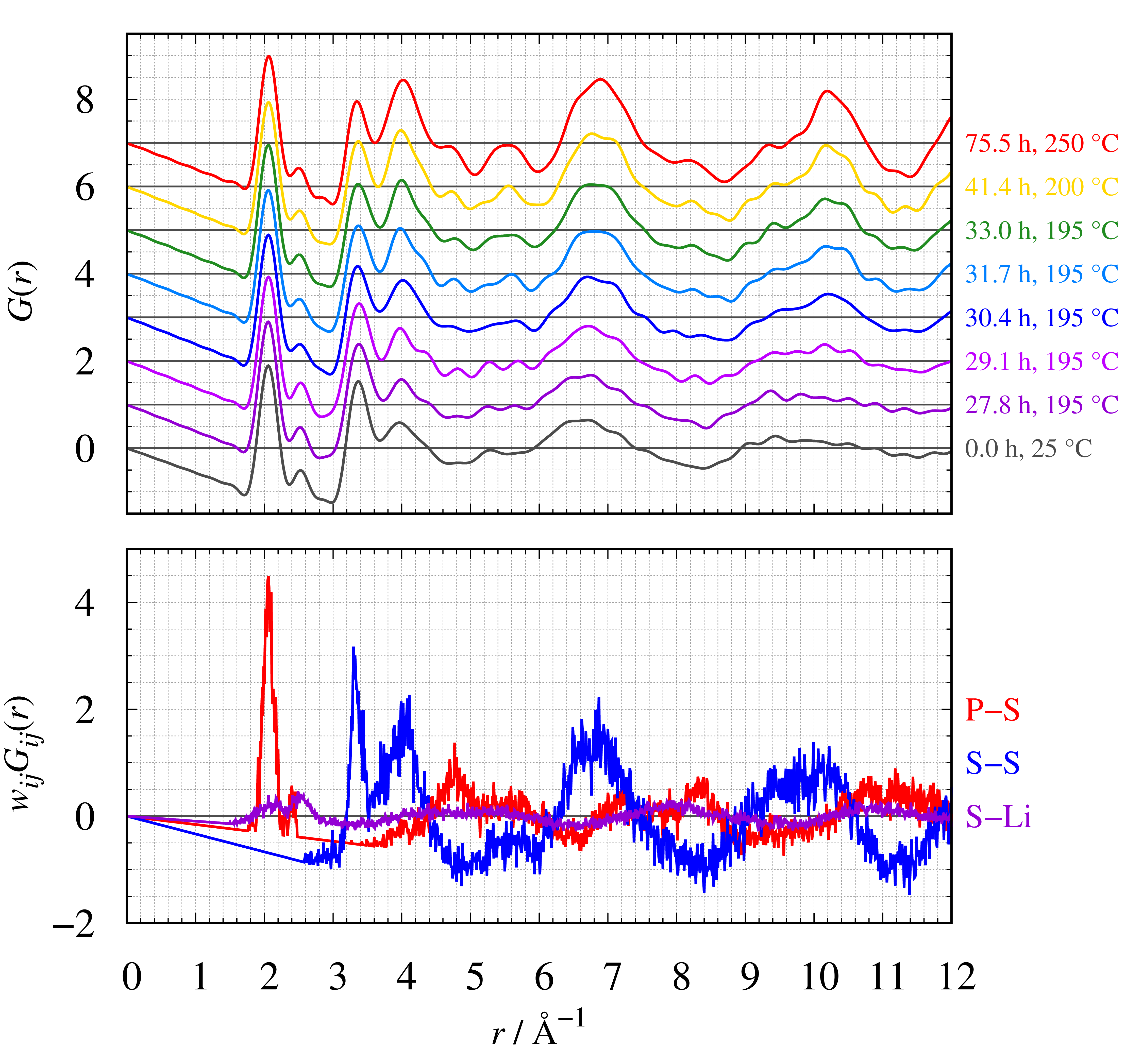
G(r)とwij Gij (r)の比較
上: 各測定時間のG(r)、下: P-S、S-S、S-Liのwij Gij (r)
下図にRMC法で得られた原子座標を単位格子に戻した原子座標を示します。一般的な傾向として、ガラスから結晶になるに従い原子の分布が狭くなっています。しかし、詳細に解析してみると、高温のガラス状態の方が室温のガラス状態と比較して僅かに原子の分布が広くなっていました。単位格子内の原子分布の解析結果傾向は、先行研究のLiイオン伝導度の結果2)と一致していました。本研究により、PS4アニオンの配置の乱れがLiイオンの伝導性に影響を与えていることが実験的に明らかになりました。
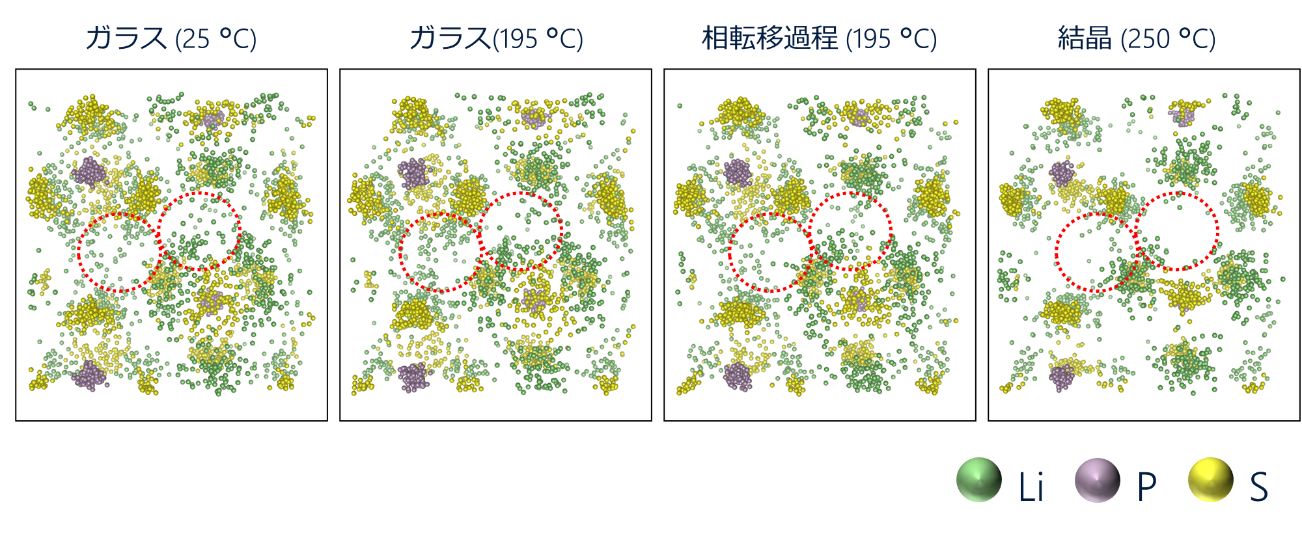
各測定温度における単位格子内の原子の分布の様子
本アプリケーションは参考文献3に詳細に記されています。
参考文献:
[1] K. Homma, M. Yonemura, T. Kobayashi, M. Nagao, M. Hirayama, R. Kanno, Solid State Ionics, 182 (2011) 53–58.doi: 10.1016/j.ssi.2010.10.001[2] S. Shiotani, K. Ohara, H. Tsukasaki, S. Mori, R. Kanno, Sci. Rep. 7 (2017) 6972 (7pp). doi: 10.1038/s41598-017-07086-y
[3] M. Yoshimoto, T. Kimura, A. Sakuda, C. Hotehama, Y. Shiramata, A. Hayashi, K. Omote, Solid State Ionics, 401 (2023), 116361 (8pp). doi: 10.1016/j.ssi.2023.116361
PDF解析に関する質問
お客様からあった質問を幾つか記載します。
Q1. ラボ機ベースのPDF解析では、$\mathrm{K\alpha}$線を単色化して$\mathrm{K\alpha_{1}}$線にしたほうが良いのか?
A. 単色化しなくて良いです。理由は実空間分解能 $\Delta r$を計算すると、仮に$\mathrm{K\alpha_{1}}$単線と$\mathrm{K\alpha}$線のデータを比較しても0.001Å以下程度の差しかない為です。 さらに$\mathrm{K\alpha_{1}}$に単色化すると強度が単色化前の1/10となり、測定時間が10倍かかります。
表. それぞれの波長における$\Delta r$
| 特性X線 | $\lambda\ (Å)$ | $Q\ (Å^{-1})$ | $\Delta r$ (Å) |
| $\mathrm{Ag\ K\alpha}$ | 0.560880 | 22.0644 | 0.1428 |
| $\mathrm{Ag\ K\alpha_{1}}$ | 0.559422 | 22.1219 | 0.1420 |
| $\mathrm{Ag\ K\alpha_{2}}$ | 0563813 | 21.9496 | 0.1431 |
Q2. 薄膜試料のPDF解析は出来ますか?
A.ラボ機では現状難しいです。MoやAg波長は侵入深さが深くなるので、薄膜以外の基板からの情報が入り込んでしまいます。
Q3. 化合物をPDF解析は出来ますか?
A. 出来ます。しかしながら、重量比や組成比によって、目的の原子間距離が見えづらくなる場合もあります。またPDFguiを用いてフィッティングすると、スケールファクターから重量比も求めることが出来ます。
Q4. PDF解析するためには大体どれくらいの測定時間ですか?
A. テスト測定では数分から10分程度です。本測定は4時間ほどかける場合が多いです。また本格的にモデリングの解析を行う場合は、1日程度かける場合もあります。求める解析や質によって、測定時間が増減します。
Q5. PDF解析にはCdTe検出器が良いと聞いたがどうですか?
A. CdTe検出器は確かに高エネルギー波長の吸収率が良いですが、検出効率は100%でないです。
また$\mathrm{Cu\ K}\alpha$のような低エネルギー波長はより検出効率が悪くなり、別検出器を用意する必要があります。
また一般的に販売されているCdTe検出器は、水冷・乾燥空気循環システムが必要になり、メンテナンス性がSi検出器よりも悪いです。
Q6. 反射法でも解析できますか?
A. 反射法でも解析は可能ですが、空気散乱などのBG成分をどのように処理するかが、少し難しいです。そのため、基本的には透過法をお勧めします。
Q7. 多元素系試料のPDFパターンから目的の原子間距離だけ抽出できますか?
A. SLS$\mathrm{I\hspace{-.01em}I}$のRMC機能やPDFguiで抽出可能です。
Q8. EXAFS(広域X線吸収微細構造)とPDFのメリット・デメリットを教えてください。
A. XAFSのメリットは元素選択性があるところです。
そのため、着目したい元素を含む相関の第1~2隣接の比較的短距離の情報を直接観測することが可能です。
EXAFSのデメリットは、長距離側のデータの信頼性が低いことや、絶対距離を得るためには位相補正が必要なことです。一方、PDFのメリットは、短距離から長距離まですべての情報を捉えることが出来るので、構造解析を行うことが出来る点です。
またEXAFSのように位相補正しなくても絶対値を算出できます。PDFのデメリットは、系内に含まれる全原子の相関が観測されてしまうことです。特に実材料のほとんどは多元素で構成されており、実測値のみでは特定の相関を抽出することができません。RMC法などを使って着目したい相関を抽出します。
表. PDFとEXAFSの特徴の比較
| EXAFS | ||
| 元素選択性 | なし | あり |
| 距離情報 | 補正無しで得られる | 位相補正が必要 |
| 得られる距離情報 | 全元素の重み付き相関 | 特定の元素の相関 |
Q9. 放射光で測定したデータをSmartLabStudio $\mathrm{I\hspace{-.01em}I}$で解析することはできますか?
A. 可能です。測定データに対して波長情報と水平偏光率を与えることで解析することができます。
Q10. 非晶質と結晶の混合物の場合、それぞれの構造情報を抽出することができますか?
A. 非晶質は結晶と比較して強度が非常に弱いため、非晶質からの情報は結晶の情報に埋もれてしまう可能性が高く、抽出が困難です。
Q11. Li₂S のLi-Li相関は観測できないのですか?
A. 結論から言うと、全散乱データやPDF解析の結果にLi-Li相関が現れることはありません。
T. E. Faber と J. M. Ziman によって、Debyeの散乱式で計算された全相関を相関別に分類(部分相関)する考え方が報告されています₁)。
この考え方で表現される構造因子やPDFは、Faber-Ziman型の構造因子・PDF と呼ばれます。
ここでは、Li₂Sを例にFaber-Ziman型構造因子の説明をします。
\begin{equation} S(Q) = \frac{c_{\mathrm{Li}}f_{\mathrm{Li}}c_{\mathrm{Li}}f_{\mathrm{Li}}}{\langle f \rangle^{2}}S_{\mathrm{LiLi}}(Q) + \frac{c_{\mathrm{Li}}f_{\mathrm{Li}}c_{\mathrm{S}}f_{\mathrm{S}}}{\langle f \rangle^{2}}S_{\mathrm{LiS}}(Q) + \frac{c_{\mathrm{S}}f_{\mathrm{S}}c_{\mathrm{Li}}f_{\mathrm{Li}}}{\langle f \rangle^{2}}S_{\mathrm{SLi}}(Q) + \frac{c_{\mathrm{S}}f_{\mathrm{S}}c_{\mathrm{S}}f_{\mathrm{S}}}{\langle f \rangle^{2}}S_{\mathrm{SS}}(Q) \nonumber \end{equation} \begin{equation} \langle f \rangle = \sum_{i}^{n}c_if_i \nonumber \end{equation}
$S(Q)$は$\mathrm{Li_{2}S}$の構造因子、$c_{i}$ と $f_{i}$ は、それぞれ$i$ 原子の濃度と原子散乱因子を示します。
さらに式中のLi-OとO-Liは等価(区別できない)なので1つにまとめることができます
\begin{equation} S(Q) = \frac{c_{\mathrm{Li}}f_{\mathrm{Li}}c_{\mathrm{Li}}f_{\mathrm{Li}}}{\langle f \rangle^{2}}S_{\mathrm{LiLi}}(Q) + \frac{2c_{\mathrm{Li}}f_{\mathrm{Li}}c_{\mathrm{S}}f_{\mathrm{S}}}{\langle f \rangle^{2}}S_{\mathrm{LiS}}(Q) + \frac{c_{\mathrm{S}}f_{\mathrm{S}}c_{\mathrm{S}}f_{\mathrm{S}}}{\langle f \rangle^{2}}S_{\mathrm{SS}}(Q) \nonumber \end{equation}
この式から全散乱強度で観測される相関は、原子の濃度と原子散乱因子を係数とした部分相関の和であることが分かります。 構造因子 $S(Q)$とPDF $G(r)$はフーリエ変換によって相互変換可能なので、$G(r)$にもFaber-Ziman型構造因子の概念を適用することができます。ただし、$G(r)$の時は原子散乱因子 $f$ の部分が原子番号 $Z$ となります。
\begin{equation} G(r) = \frac{c_{\mathrm{Li}}Z_{\mathrm{Li}}c_{\mathrm{Li}}Z_{\mathrm{Li}}}{\langle Z \rangle^{2}}G_{\mathrm{LiLi}}(r) + \frac{2c_{\mathrm{Li}}Z_{\mathrm{Li}}c_{\mathrm{S}}Z_{\mathrm{S}}}{\langle Z \rangle^{2}}G_{\mathrm{LiS}}(r) + \frac{c_{\mathrm{S}}Z_{\mathrm{S}}c_{\mathrm{S}}Z_{\mathrm{S}}}{\langle Z \rangle^{2}}G_{\mathrm{SS}}(r) \nonumber \end{equation} \begin{equation} \langle Z \rangle = \sum_{i}^{n}c_iZ_i \nonumber \end{equation}
表にLi₂Sの部分相関のFaber-Ziman型構造因子の係数をまとめました。
Li-Liは全体の7%程度しか含まれていないので、実際の$G(r)$でLi-Li相関のみのピークを観測することは難しそうだということが分かります。
表 $\mathrm{Li_{2}S}$の$G(r)$におけるFaber-Ziman係数
| 相関 | Li-Li | Li-S | S-S |
| 係数 % | 7.44 | 39.67 | 52.89 |
最後に、Faber-Ziman型構造因子およびPDFの一般形を載せておきます。
$S(Q)$の場合、
\begin{equation} S(Q)=\sum_{i, j\ge i}(2-\delta_{ij})\frac{c_{i}f_{i}c_{j}f_{j}}{\langle f \rangle} S_{ij}(Q) \nonumber \end{equation}
$G(r)$の場合、
\begin{equation} G(r)=\sum_{i, j\ge i}(2-\delta_{ij})\frac{c_{i}Z_{i}c_{j}Z_{j}}{\langle Z \rangle} G_{ij}(r) \nonumber \end{equation}
$\delta_{ij}$ はクロネッカーのデルタです。したがって同種原子の相関は $(c_{i}f_{i}c_{j}f_{j})/\langle f \rangle$ となり、異種原子間は $(2c_{i}f_{i}c_{j}f_{j})/\langle f \rangle$ となります。
参考文献:
[1] T. E. Faber and J. M. Ziman, Phil. Mag., 11(1965), 153-173. (https://doi.org/10.1080/14786436508211931)
RMC法について
Reverse Monte-Carlo RMC 法は、R. L. McgreevyとL. Putzaiらによって報告された実測値を再現する構造モデルを探査する手法であり、当初は液体や非晶質の構造探査手法としてよく使われていました1)。 しかし、A. Mellergård とR. L. McgreevyによってRMCPOW法2) 、 M. G. TuckerらによってRMCProfile法3) が報告されてから結晶性材料の局所構造解析にも盛んにRMC法が使われるようになりました。 結晶性材料のPDF解析のツールとして広く知られているPDFFIT 4) や PDFgui 5) は実測値のG(r) を再現するために単位格子を使用することから”Small Box Simulation”と呼ばれています。 一方、RMCでは実測値を再現に大きな計算ボックスを必要とするため”Large Box Simulation”と呼ばれています。
なぜRMC法を使うのか?
RMC法を使うことで、実測値から得られない実空間情報: 1. 構造モデル、2. 部分相関、3: 角度ヒストグラムなどの情報が得ることができます。
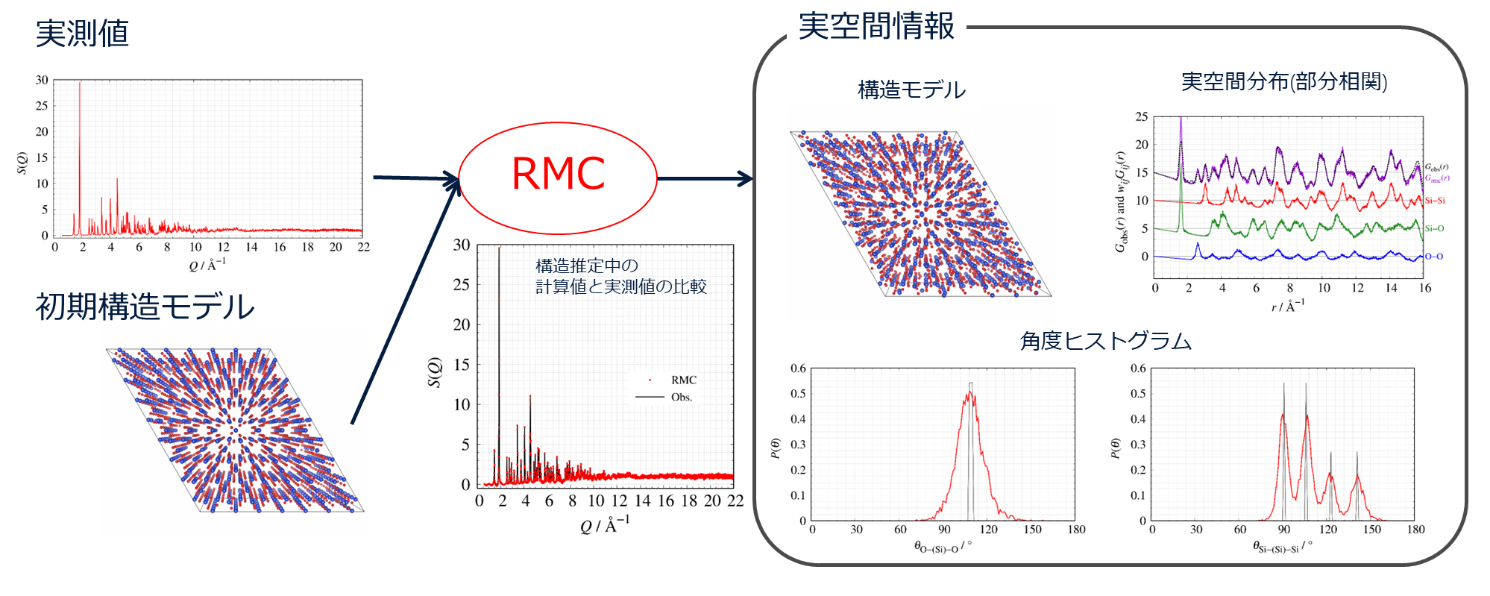
RMC法による構造モデリングの概略図
基本的なRMC法の計算の流れ
RMC法を知るうえで重要な式は2つあります。初めに式1に示すのは原子配置から散乱強度を計算する式で、
\begin{equation} S_{\mathrm{RMC}}(Q) = \rho_0 \displaystyle \int_{0}^{r_{\mathrm{max}}} 4πr^2 (g_{\mathrm{RMC}} (r)-1) \frac{{\mathit{\sin{Qr}}}}{\mathit{Qr}} \mathit{dr}\end{equation}
ここで、$\rho_{0} = N/V$ は数密度 ($N$: 計算ボックス内の原子(粒子)の個数、$V$: 計算ボックスの体積、$r_{\max}$: RMC法での最大の計算距離(一辺$L$の立方体の計算セルなら、$r_{\max} = L/2$)、$Q$は散乱ベクトルです。)
式2に示すのは実測値と計算値から構造モデルを評価する式で、
\begin{equation} x^2 = \displaystyle \sum_{i=1}^{N} \frac{(S_{\mathrm{obs}}(Q_i)- S_{\mathrm{RMC}}(Q_i))^{2}}{\sigma^{2}(Q_i)} \end{equation}
RMC法の計算中の試行は全て乱数により制御されています。
- 移動させる原子(または粒子)をランダムに選択し、微小移動量を生成します。
- 移動後の原子配置から計算値(S(Q)またはG(r))が実測値とのカイ2乗値が
●小さくなる: 1の試行を採択
●大きくなる: 1の試行を棄却 - 1, 2の手順をカイ2乗値が目標値を下回るまで繰り返し実行します。
実際のRMCの計算の様子
RMC法実行時のS(Q)、G(r)と構造モデルの変化
参考文献:
[1] R.L. McGreevy, L. Pusztai, Molec. Simul. 1 (1988) 359-367. doi: 10.1080/08927028808080958[2] A. Mellergård ,R. L. McGreevy, Acta Crystallogr. A 55 (1999) 783-789. doi: 10.1107/S0108767399000197
[3] M.G. Tucker, D.A. Keen, M.T. Dove, A.L. Goodwin, Q. Hui, J. Phys.: Condens. Matter. 19 (2007) 335218. doi: 10.1088/0953-8984/19/33/335218
[4] Th. Proffen, S.J.L. Billinge, J. Appl. Crystallogr. 32 (1999) 572-575. doi: 10.1107/S0021889899003532
[5] C.L. Farrow, P. Juhas, J.W. Liu, D. Bryndin, E.S. Božin, J. Bloch, T. Proffen, S.J.L. Billinge, J. Phys.: Condens. Matter. 19 (2007) 335219. doi: 10.1088/0953-8984/19/33/335219
本サイト内での構造モデル図はVESTA 3を使って描画しています, K. Momma and F. Izumi, J. Appl. Crystallogr. , 44(2011) 1272-1276. (doi:10.1107/S0021889811038970)
